Pruebas de proyectiles navales de 120 mm y 6 mm 1901-1903. en la armadura Krupp

En este artículo veremos los resultados de las pruebas de proyectiles de 120 mm y 152 mm con puntas perforantes.
Acerca de las tablas de datos
Antes de pasar a las tablas propiamente dichas, creo que es necesario dar algunas explicaciones. Para reducir su tamaño, pero al mismo tiempo mantener el máximo contenido informativo, no anoté su nombre completo en la columna “número de losa”, sino que me limité a consultar el número de serie de la tabla publicada en el artículo anterior. . Para que el respetado lector no tenga que buscarlo en los materiales, lo vuelvo a presentar.
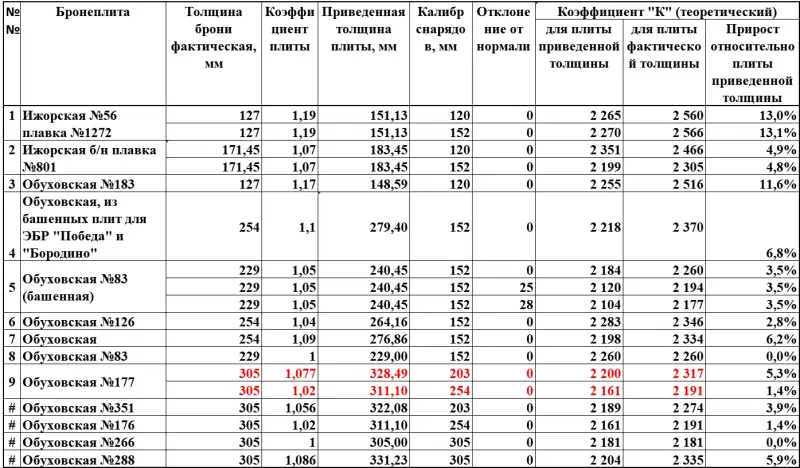
Los datos disponibles presentan pruebas de proyectiles de las plantas de Obukhov, Perm y Putilov equipados con puntas perforantes. Debido a que la calidad de estos proyectiles puede variar, he agrupado los resultados de las pruebas por fabricante del proyectil.
Indicaré sólo el espesor real de la losa en las tablas de prueba; el espesor dado para cada losa se puede ver arriba.
La columna "Velocidad real de la armadura" contiene la velocidad del proyectil en el momento del impacto sobre la armadura, que tenía durante las pruebas.
La columna "Velocidad calculada para un proyectil sin punta" contiene información a qué velocidad mínima debería haber penetrado un proyectil de un peso determinado en esta losa en particular. Además, si el coeficiente de la losa es mayor que el estándar, entonces la velocidad será mayor que la que sería suficiente para atravesar una losa de un espesor determinado y una durabilidad estándar. Permítanme recordarles que esta velocidad la calculé durante las pruebas y no yo personalmente.
La columna "Reducción de la velocidad en relación con la calculada" muestra cuánto por ciento es menor la velocidad real del proyectil al golpear la placa que la calculada para un proyectil sin punta. En consecuencia, si un proyectil con punta, después de la prueba, penetra la armadura en el límite, o muy cerca de ella, entonces esta reducción de velocidad es un indicador de la efectividad y el resultado de la punta perforadora.
El estimado lector puede hacer una pregunta: ¿por qué es necesario este indicador de "reducción de la velocidad en relación con la calculada"? Hay una velocidad de proyectil en la armadura, entonces, ¿por qué dividir los pelos?
El hecho es que la capacidad de un proyectil para penetrar la protección depende de muchos parámetros, incluida la masa del proyectil, el grosor y la durabilidad de la armadura. Pero la velocidad del proyectil sobre la armadura no tiene nada de esto en cuenta. Los proyectiles varían ligeramente en peso, y un proyectil más ligero necesita un poco más de velocidad para penetrar el mismo espesor de armadura que uno más pesado. Si tomamos un proyectil del mismo peso, para penetrar, digamos, 229 mm de armadura de resistencia estándar, se requerirá una velocidad inicial, pero si la resistencia de la armadura es mayor, entonces se necesitará otra, mayor.
El indicador "Velocidad en armadura" ignora todo esto. El indicador "Reducción de velocidad con respecto a la calculada", por el contrario, también tiene en cuenta la influencia del peso de los proyectiles, los diferentes espesores y durabilidad de las placas de blindaje y, al mismo tiempo, el ángulo de desviación de lo normal en los casos en que uno estaba presente.
En la columna "Coeficiente "K" para parámetros reales", el valor del coeficiente "K" se calcula utilizando la fórmula de De Marre para espesores/velocidades de armadura reales y masas de proyectiles. Este significado nos dice lo siguiente: "Si un proyectil con tales datos iniciales penetrara el blindaje hasta el límite, esto significaría que el coeficiente "K" de este blindaje es igual al valor especificado".
Creo que el significado de las columnas restantes es obvio y no necesita explicación.
Resultados de las pruebas de proyectiles de 120 mm.

Entonces, como puede verse en la tabla, se dispararon proyectiles de 120 mm contra 3 placas de blindaje, de los cuales 2 tenían un espesor de 127 mm y uno de 171,45 mm. Y la enorme diferencia en los resultados del bombardeo de losas de 127 mm y de 171,45 mm llama inmediatamente la atención. Sólo queda afirmar cuán inexacto puede ser un intento de determinar la resistencia de la armadura de un tipo u otro si se realiza con material estadístico limitado.
Supongamos que tuviéramos a nuestra disposición datos de disparos exclusivamente en la losa número 1. En este caso, la conclusión sería completamente obvia: los disparos número 4 y 5, como resultado de los cuales se perforaron tanto la losa como el marco, y el proyectil, permaneciendo intacto, voló a 92 m, muy cerca de la máxima penetración de blindaje.
En otras palabras, la resistencia del blindaje contra un proyectil con una punta perforadora se puede evaluar como una "K" de poco menos de 1-854 y se puede reconocer que la punta proporcionó una reducción en la velocidad necesaria para penetrar el blindaje. placa en poco más de 1-881%. Sólo podemos concluir que la punta "Makarov" fue al menos dos veces más efectiva que las estadounidenses: los estadounidenses no tenían armas de 26,5 mm, pero el uso de puntas perforantes en proyectiles de cinco pulgadas en armaduras de cinco pulgadas proporcionó , según sus estándares, una reducción de la velocidad del 27,6%.
Si consideramos un solo disparo (N° 10) disparado contra la placa de blindaje N° 127 de 3 mm, entonces, aunque con algunas reservas, corresponde aproximadamente a los resultados de los disparos N° 1 y 2. Por supuesto, hay una desviación, pero está dentro de lo razonable.
Pero si nos fijamos en los resultados de disparar contra la placa de blindaje número 2 más gruesa, la imagen es completamente diferente.
Después de todo, si se atravesó una placa de 127 mm incluso cuando la velocidad se redujo al 26-27% del valor calculado, entonces una placa de 171,45 mm con una reducción de velocidad de sólo 12,4-12,7% debería haber sido fácilmente atravesada, y El proyectil debería haber mirado a más de un kilómetro detrás de él. Mientras tanto, como se desprende de los planos 8 y 9, no hubo nada parecido: sólo en un caso el proyectil logró superar la losa y el marco, pero en ambos casos no hubo una penetración clara: los proyectiles se rompieron.
Entonces resulta que, evaluando la durabilidad de la placa de armadura en relación con un proyectil con una tapa perforante y la efectividad de la punta "Makarov", obtenemos:
• para una placa de blindaje de 127 mm: “K” inferior a 1–854 y una reducción de la velocidad necesaria para penetrar la placa entre un 1 y un 894%;
• para una placa de blindaje de 171,45 mm: “K” más de 2–152 y una reducción de la velocidad necesaria para penetrar la placa en menos del 2%.
Y este último ya se acerca a los estándares estadounidenses: según ellos, la reducción correspondiente en la velocidad para un proyectil de cinco pulgadas y un blindaje de seis pulgadas fue del 11,59%; lamentablemente, no se da una evaluación de la efectividad para un blindaje de siete pulgadas. Obviamente será menor, ya que los estadounidenses también observaron la dinámica de una disminución en la efectividad de la punta perforadora al aumentar el espesor del blindaje.
También cabe destacar la cercanía de los parámetros en los que la placa es perforada por un proyectil, que se destruye al ser superado, y por proyectiles, que, aunque superan el blindaje hasta el límite, permanecen intactos. Para una placa de 127 mm en "K" = 1-854, los proyectiles penetran intactos el blindaje hasta el límite, y ya en "K" = 1 el proyectil se rompe. Esto es lógico, ya que en el segundo caso las condiciones para el proyectil son ligeramente peores que en el primero.
Pero para un blindaje con un espesor de 171,45 mm, un proyectil con “K” = 2 no penetra el blindaje y se rompe, mientras que en condiciones ligeramente peores (“K” = 152) aunque se rompió solo, aún así hizo agujeros tanto en el casa de placas y troncos
Es fácil encontrar una explicación para estas pequeñas desviaciones, aunque aparentemente ilógicas: aquí un caparazón ligeramente mejor, allí una sección de la placa de armadura un poco menos resistente fue atrapada, aquí la precesión y la nutación jugaron un pequeño papel, etc.
Pero veamos las pruebas de munición de seis pulgadas.
Resultados de las pruebas de proyectiles de 152 mm.
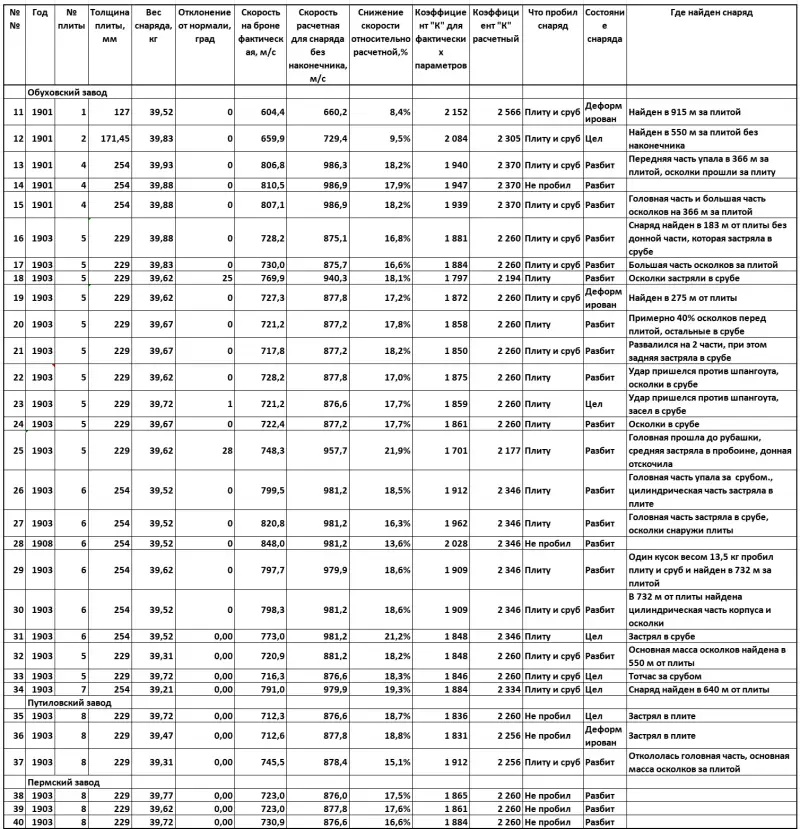
Consideremos primero los resultados del bombardeo de la losa n° 5 (torre Obukhovskaya n° 83) con proyectiles Obukhov de seis pulgadas. A primera vista, parece bastante obvio que el resultado más cercano a la máxima penetración del blindaje lo mostró el disparo número 23: el proyectil atravesó la losa y permaneció intacto, pero, al golpear frente al marco, se atascó en el marco. En este caso, “K” = 1, la velocidad es un 859% inferior a la calculada. En realidad, estos son los resultados que deberían tomarse como modelo.
Pero miremos simplemente los resultados de otros proyectiles.
Miremos el impacto número 24: con la misma disminución de velocidad en relación con la calculada (17,7%), el proyectil pudo atravesar la losa, pero nuevamente se estrelló. Bueno, supongamos que una disminución de la velocidad del 17,7% de la calculada es precisamente el límite en el que la naturaleza probabilística de la penetración del blindaje lleva al hecho de que en un caso el proyectil penetrará el blindaje intacto y, en el otro, roto. .
Esto significa que con una menor disminución de velocidad, el proyectil penetrará con confianza la armadura y pasará detrás de ella como un todo, ¿verdad?
Parece que el plano nº 19 confirma brillantemente esta teoría. La velocidad se reduce no en un 17,7%, sino en un 17,2% de la calculada, coeficiente “K” = 1, el proyectil penetra tanto en la losa como en el marco, y, aunque deformado, ¡se encuentra a 872 m de la losa! Es decir, la losa se rompe con un gran margen...
Pero luego llegó al número 22. La velocidad no se redujo en un 17,7% ni en un 17,2%, sino sólo en un 17% de la calculada. Uno esperaría que el proyectil atravesara la armadura, el armazón y volara hacia el hermoso mundo tan lejano que no lo encontraríamos en el sitio de prueba. Pero no, el caparazón, tras perforar la losa, se rompió y el marco quedó sin perforar.
Bueno, ¿tal vez el proyectil fue atrapado con algún tipo de defecto interno y por eso rompe las estadísticas?
Bueno, veamos las tomas 16 y 17. La velocidad no se ha reducido ni siquiera en un 17%, sino sólo entre un 16,6% y un 16,8% de la calculada, y parece que se debe esperar que estos proyectiles perforen tanto la losa como la casa de troncos y se vayan volando a países lejanos. Sólo que, contrariamente a nuestras expectativas, en ambos casos los proyectiles se estrellaron.
Bueno, entonces tal vez deberíamos suponer que los proyectiles de los disparos n.° 16, 17 y 22 eran de calidad estándar, y que el disparo n.° 23, que identifiqué por primera vez como estándar, era anormalmente bueno.
Para probar esta hipótesis, mire ahora la toma número 33.
La velocidad se redujo hasta un 18,3% de la calculada. Bueno, aquí el proyectil, obviamente, no debe rebotar en la losa como un guisante en la pared, y luego ciertamente no perforarla. Pero el resultado fue completamente diferente: la carcasa permaneció intacta y la losa y el marco se rompieron. Es decir, si consideramos que la toma número 23 es anormalmente buena, entonces ésta es súper anormalmente buena, ¿verdad?
En otras palabras, parece haber muchas estadísticas, pero en lugar de una tendencia hay un caos total. Y esto a pesar de que en todos los casos anteriores se garantiza la máxima convergencia de datos: todos estos disparos se realizaron en la misma placa de blindaje (torreta Obukhovskaya n.° 83, 229 mm), con proyectiles de la misma planta de Obukhov, en mismo ángulo.
¿Y si cogemos las mismas conchas, pero con un plato diferente?
Comparemos las tomas n.° 33 y n.° 34.
El proyectil número 33, anteriormente considerado "súper anormalmente bueno", con una disminución de velocidad del 18,3%, perfora la losa, la casa de troncos y cae inmediatamente detrás de la casa de troncos. En consecuencia, con el disparo número 34, el proyectil no se disparó contra la placa número 5, sino contra la placa número 7, que, por cierto, como la placa número 5, fue producida por la planta de Obukhov, con una disminución en la velocidad de el calculado en un 19,3%, parece que no puede atravesar la losa, y si por algún milagro lo hace, se desmoronará. Mientras tanto, no sólo atravesó la losa y el marco, sino que voló 640 m ¡permaneciendo intacto!
En otras palabras, los resultados de esta toma contradicen completamente todo lo que observamos antes, y la cuestión es que la placa es diferente. Aunque del mismo fabricante.
Sin embargo, todavía podemos concluir que "K" es de alrededor de 1 y la eficiencia de la punta "Makarov" es aproximadamente un 860% de reducción de velocidad con respecto a la calculada. Con suposiciones y como algo intermedio. Y este es un gran resultado, pero...
Tomemos otra losa de la planta de Obukhov, del mismo espesor que la anterior: 229 mm. Y proyectiles del mismo calibre de 152 mm, pero producidos por otra planta: Perm. Y veremos que los proyectiles de la planta de Perm (disparos nº 38–40), con prácticamente los mismos parámetros (“K” = 1–861) y una reducción de la velocidad respecto a la calculada en un 1–884%, no penetre nada en absoluto: en los tres casos la losa está intacta, las cáscaras están rotas. Lo que contradice completamente los logros de los proyectiles fabricados por Obukhov.
Sólo queda afirmar que las cáscaras de la planta de Perm son mucho peores que las de Obukhov, y esto explica un resultado tan desastroso.
Los proyectiles de la planta de Putilov, cuando la velocidad disminuye con respecto a la calculada entre un 18,7% y un 18,8%, no atraviesan las placas de blindaje de 229 mm y se rompen (disparos nº 38-39). Esto no contradice los resultados discutidos anteriormente. Sin embargo, con una velocidad reducida del 15,1%, el proyectil de la planta Putilov perfora la losa y el marco, pero se rompe.
Y si solo tuviéramos a nuestra disposición pruebas de estos proyectiles, entonces concluiríamos que la punta perforadora podría penetrar el blindaje con cierta confianza solo si la velocidad del proyectil se redujera en un 14 por ciento, ciertamente no menos, y tal vez se requeriría una mayor velocidad de proyectil en la armadura. Pero, habiendo probado los proyectiles Perm y Obukhov, podemos suponer que los proyectiles Putilov también eran inferiores en calidad a los proyectiles Obukhov.
También es digno de mención la completa confusión sobre la cuestión de la penetración del proyectil a través de la armadura en su conjunto.
Si nos fijamos en los disparos nº 13 a 30, entonces parece desarrollarse la siguiente dinámica: con una disminución de la velocidad entre un 17 y un 18% con respecto a la calculada, en general, aunque los proyectiles perforan la armadura, ellos mismos se rompen, aunque en Casos aislados (Nº 23) todos pasan por la armadura en su conjunto. Es obvio que cuanto mayor es la velocidad, mayores son las posibilidades de que el proyectil atraviese la armadura por completo, y está claro que cuando la velocidad disminuye de la calculada en un 8-10%, los proyectiles penetran bien la armadura y permanecen intactos. (disparos nº 11-12). En consecuencia, se podría suponer que con una disminución de la velocidad del 13 al 15% del valor calculado, los proyectiles atravesarían con confianza toda la armadura.
Sin embargo, si miramos los disparos 31-36, veremos que los proyectiles de repente permanecen intactos incluso cuando la velocidad se reduce al 18-19% de la calculada, y en un caso incluso al 21,2%, aunque no Siempre en esto es capaz de penetrar la armadura.
Cuando la velocidad disminuyó en relación con la calculada en un 17-18%, los proyectiles Obukhov generalmente penetraban la armadura, incluso siendo destruidos en el proceso, mientras que los proyectiles Putilov, sin penetrar, permanecían intactos. Pero los proyectiles Perm no pudieron penetrar la armadura y ellos mismos fueron destruidos.
Y sin embargo hay una tendencia
Excluimos las estadísticas de los proyectiles Perm, presumiblemente de mala calidad, así como el disparo a una placa de 127 mm, que dio un resultado excesivamente bueno. En este caso, las pruebas de proyectiles de 152 mm dan la siguiente dinámica:
1. En el intervalo “K” = 1–701 (1 unidades), se perfora el blindaje, pero el proyectil se parte y no se puede atravesar el blindaje en su conjunto. Se registran casos de no perforación de armaduras (“K” = 883 y 182).
2. En el intervalo “K” = 1–884 (1 unidades), los proyectiles a veces penetran el blindaje en su totalidad y a veces son destruidos en el proceso. Se registró un caso de falla del blindaje en “K” = 962.
3. En el intervalo “K” = 1-963 (2 unidades), los proyectiles penetran con seguridad el blindaje en su conjunto. Sin embargo, incluso aquí se registró un caso de falla del blindaje en “K” = 084.
Es decir, el blindaje fue penetrado en el gigantesco rango “K” de 1 a 701 (2 unidades) y, aunque es posible identificar claramente zonas donde el proyectil se rompe/puede romper o no rompe/no rompe, en Por suerte para el defensor, es posible que el proyectil no penetre la armadura en absoluto.
Si recordamos que los cambios en el coeficiente “K” son proporcionales a la velocidad del proyectil sobre el blindaje necesaria para atravesarlo, y tomando como 100% la velocidad mínima registrada en las pruebas en las que el proyectil apenas traspasó el blindaje y se estrelló, tenemos conseguir:
1. Cuando la velocidad aumenta del 0% al 10,7% del mínimo, el proyectil penetra la armadura, pero al mismo tiempo se rompe.
2. Cuando la velocidad aumenta por encima del 10,7% al 15,29% del mínimo, el proyectil penetra el blindaje, a veces rompiéndose, a veces en su totalidad.
3. Con un aumento de velocidad del 15,29% al 22,4% del mínimo, el proyectil atraviesa el blindaje y permanece intacto.
Hallazgos
Penetrar una armadura con un proyectil es un proceso físico complejo que obviamente depende de muchas variables. La calidad del material y el endurecimiento de las placas de blindaje no pueden ser absolutamente iguales (aparentemente, incluso dentro de la misma placa), y lo mismo ocurre con los proyectiles: uno es un poco mejor y el otro un poco peor, aunque se fabricaron con la misma tecnología.
Sin duda, también existen ciertas desviaciones tanto en la masa del proyectil como en las cargas de pólvora que hacen volar estos proyectiles. Y esto, por supuesto, afecta la velocidad a la que el proyectil golpea la armadura. El eje del proyectil que sale del cañón del arma, aunque ligeramente, cambia su dirección con respecto al vector de movimiento en el espacio (precesión), razón por la cual la posición de los proyectiles, incluso si se disparan en un ángulo de 90 grados con respecto a la placa. , en el momento del impacto en la armadura puede diferir.
Sin lugar a dudas, si en algún modelo ideal fuera posible eliminar todas estas desviaciones y disparar proyectiles absolutamente equivalentes en todos los aspectos a velocidades absolutamente idénticas con placas de blindaje idealmente equivalentes, entonces la fórmula de De Marr daría un valor completamente preciso para la velocidad. en el que un proyectil penetra la armadura dado el espesor en el límite.
Por debajo de esta velocidad, el proyectil podría perforar la armadura, colapsando en el proceso, y con un aumento de velocidad, siempre perforaría la armadura, pasando más allá de ella en su totalidad. Pero incluso en este caso, disparar los mismos proyectiles ideales contra una placa de blindaje más gruesa o más delgada, incluso si está hecha de un material de idéntica resistencia, ya implicará ciertos ajustes.
Pero en realidad, esos ideales son, por supuesto, inalcanzables.
Y los resultados de las pruebas de proyectiles de 120 mm y 6 pulgadas indican claramente que:
1. No existe un límite claro de velocidad (o coeficiente "K", si se prefiere), que separe la penetración de la no penetración, el paso a través del blindaje en general del paso detrás del blindaje cuando se destruye un proyectil, en condiciones reales.
2. Hay una “zona inferior”, dentro de la cual el proyectil penetra el blindaje, rompiéndose, una “zona superior”, en la que penetra el blindaje, permaneciendo intacto, y una “zona gris” entre estas dos zonas, donde el El paso detrás de la armadura en su conjunto o con la destrucción del proyectil son igualmente probables. Sin embargo, en cualquiera de estas zonas, el blindaje no puede ser penetrado periódicamente.
3. Las dimensiones de estas zonas son extremadamente grandes: si tomamos como base la velocidad del proyectil en el medio de la zona "gris", entonces los límites de las zonas "inferior" y "superior" están a más del ±10% de el cambio en esta velocidad.
4. Para determinar con mayor o menor precisión los límites de las áreas de penetración, se necesita material estadístico en docenas de disparos realizados en condiciones similares: el mismo tipo de armadura y proyectiles, un ángulo similar de desviación de lo normal.
5. El resultado de los cálculos de De Marr para proyectiles equipados con casquillos perforantes está significativamente influenciado por el calibre del proyectil y el espesor del blindaje. El coeficiente "K" calculado para proyectiles de 120 mm y blindaje de 127 mm tampoco se puede extrapolar a los mismos proyectiles cuando "trabajan" con un blindaje de 171,4 mm, y mucho menos a proyectiles de 6 mm probados según un blindaje de 171,45, 254-XNUMX mm.
Eso sí, hay que tener en cuenta que el uso de proyectiles con casquillos perforantes mod. 1911 o después, así como los proyectiles sin casquillo, podrían dar estadísticas diferentes. Pero hay que suponer que el principio de formación de las zonas "superior", "inferior" y "media" seguirá siendo el mismo.
En cuanto a la efectividad de las puntas "Makarov", sacaré conclusiones después de demostrarle al querido lector los resultados de las pruebas de proyectiles de 8 dm, 10 dm y 12 dm.
To be continued ...
información